Linear System With Infinitely Many Solutions
Linear system with infinitely many solutions. Answer 1 of 2. The matrix equation Axb has a solution if and only if b is a linear combination of the columns of A. If the system has infinitely many solutions describe the solution with the equation of a plane or an ordered triple in terms of one variable 3x 6y - 92 15 - x - 2y 3z -5 X 2y - 3 - 5 A.
So an equation with infinitely many solutions essentially has the same thing on. The system has infinitely many. Find the complete solution of the linear system or show that it is inconsistent.
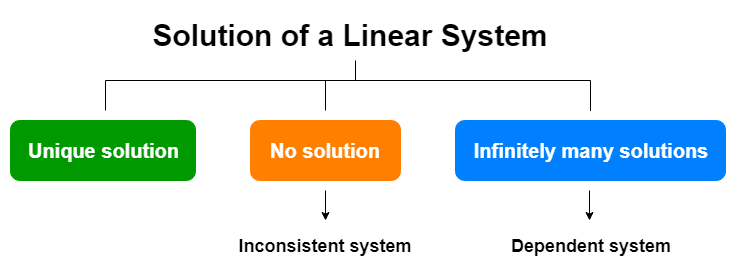
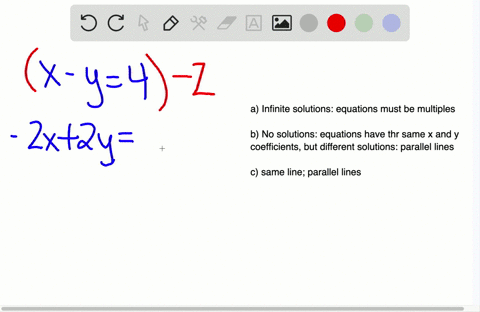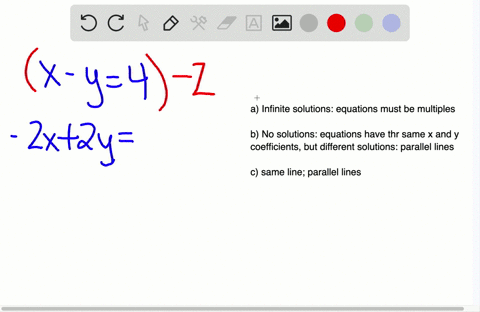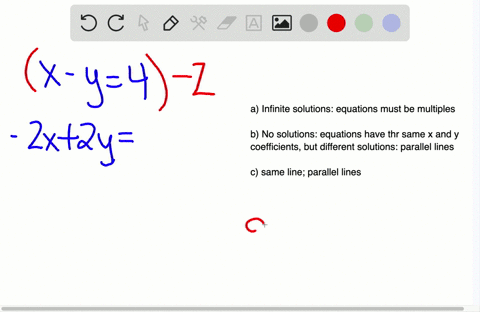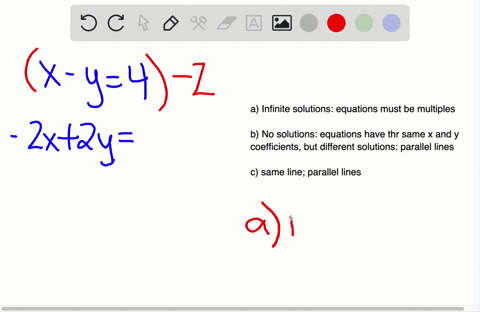
A consistent pair of linear equations will always have unique or infinite solutions. Example 1 Here are two equations in two variables. There could be zero one or infinitely many solutions.
A1x b1y c1 - 1 a2x b2y c2 - 2 If a1a2 b1b2 c1c2 Then the equation is a consistent and dependent equation which has infinitely many solutions. The question asks to find equation for which the system has infinitely many solutions. For example is not a solution to the system below but that does not mean that it has no solution.
In this article we will see this by solving an example. Given a linear system of three equations solve for three unknowns. It means that displaystyleqquadbeginaligna_11x_1 dots a_1nx_n b_1 vdots a_n1.
Solve the system of linear equations. Solving linear systems with infinitely many solutions. Were asked to use the drop-down to form a linear equation with infinitely many solutions.
If A x b and A 0 then A 1 does not exist. If A x b and A 0 then A 1 exists so x A 1 b is the unique solution of the system.
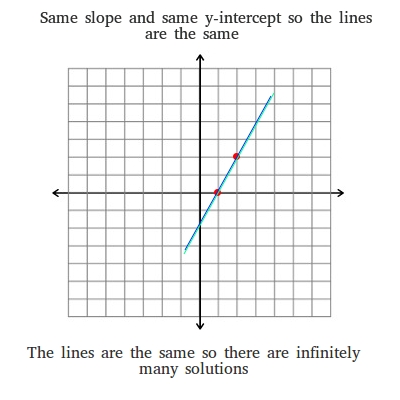
This means that any point on the line is a solution to the system.
An equation can have infinitely many solutions when it should satisfy some conditions. Consider the system of one equation with two unknowns 0x0y1 This system has no solution at all. The unique solution to the system is CD Type an exact answer in. Example of solving a 3-by-3 system of linear equations by row-reducing the augmented matrix in the case of infinitely many solutions mathlaelinsys3x3solnrow_reducei. Lets see what will happen when we try to solve the following linear system with NumPy. This means that A y 0 for some nonzero vector y A has linearly dependent columns. When a system of linear equations has infinitely many solutions such a system is called a dependent system. This means there are infinitely many points all on a line which lie on all three planes. In other words they are the same exact line.
Hidden-answer Using the method of addition. When a system of linear equations has infinitely many solutions such a system is called a dependent system. When an unknown variable solution depends on another unknown then the system is called linear system with infinitely many solutions. Given a linear system of three equations solve for three unknowns. Consider the system of one equation with two unknowns 0x0y1 This system has no solution at all. Answer 1 of 2. It means that it either has infinitely many solutions or no solutions.

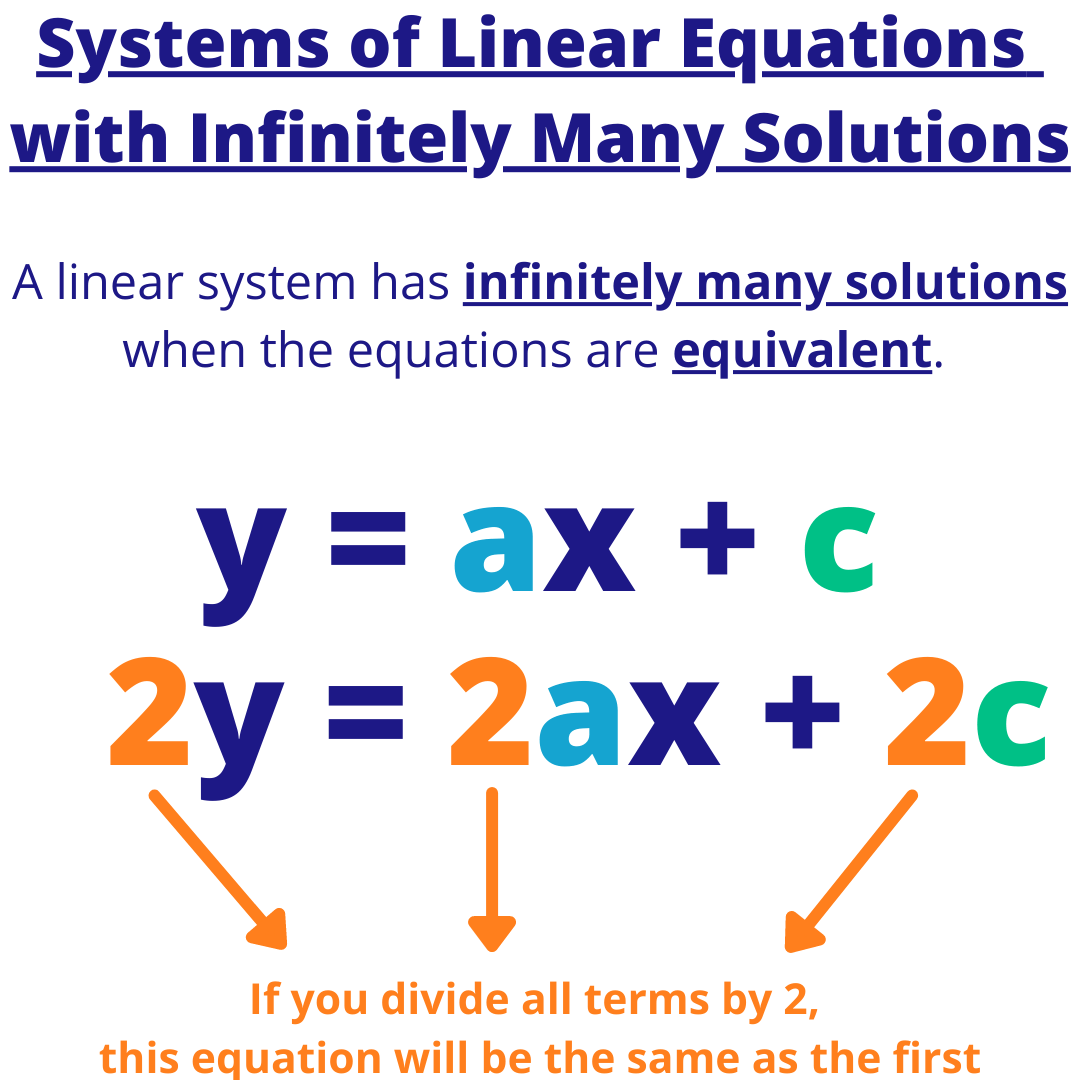
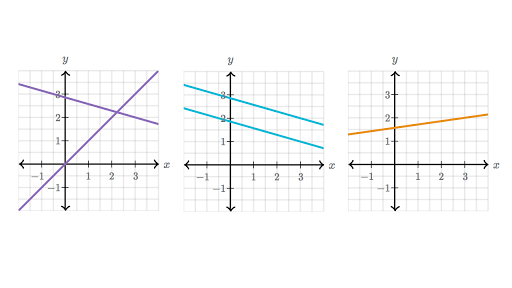


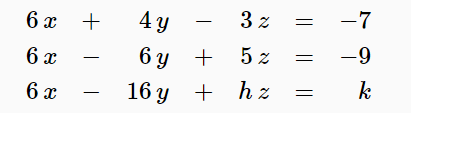



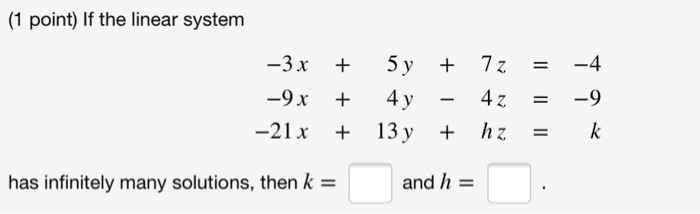
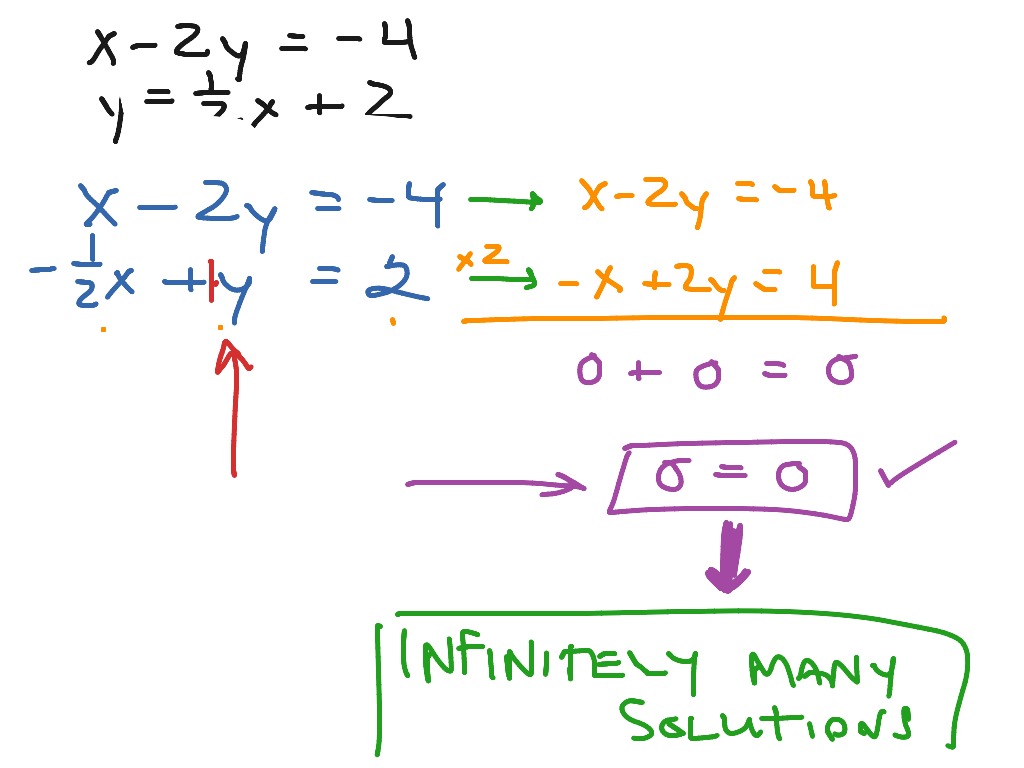













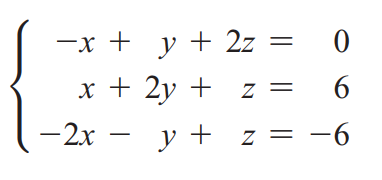











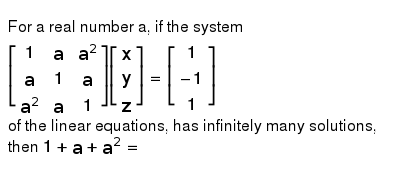

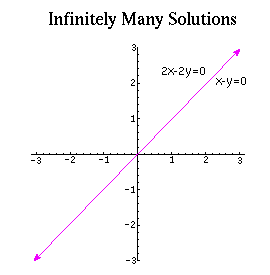




Post a Comment for "Linear System With Infinitely Many Solutions"